Using Concrete Scales: A Framework for Visual Depiction of Complex Measures

From financial statistics to nutritional values, we are frequently exposed to quantitative information expressed in measures of either extreme magnitudes or unfamiliar units, or both. A common practice used to comprehend such complex measures is to relate, re-express, and compare them through visual depictions using magnitudes and units that are easier to grasp. Through this practice, we create a new graphic composition that we refer to as a concrete scale. To the best of our knowledge, there are no design guidelines that exist for concrete scales despite their common use in communication, educational, and decision-making settings. We attempt to fill this void by introducing a novel framework that would serve as a practical guide for their analysis and design. Informed by a thorough analysis of graphic compositions involving complex measures and an extensive literature review of scale cognition mechanisms, our framework outlines the design space of various measure relations---specifically relations involving the re-expression of complex measures to more familiar concepts---and their visual representations as graphic compositions.

Visual Language

One of the main contribution of the paper is to introduce a visual language as a mechanisms to support a systematic break down of visual material related to scale explanation. While the language can get complex, the main graphic decomposition mechanisms are as below:

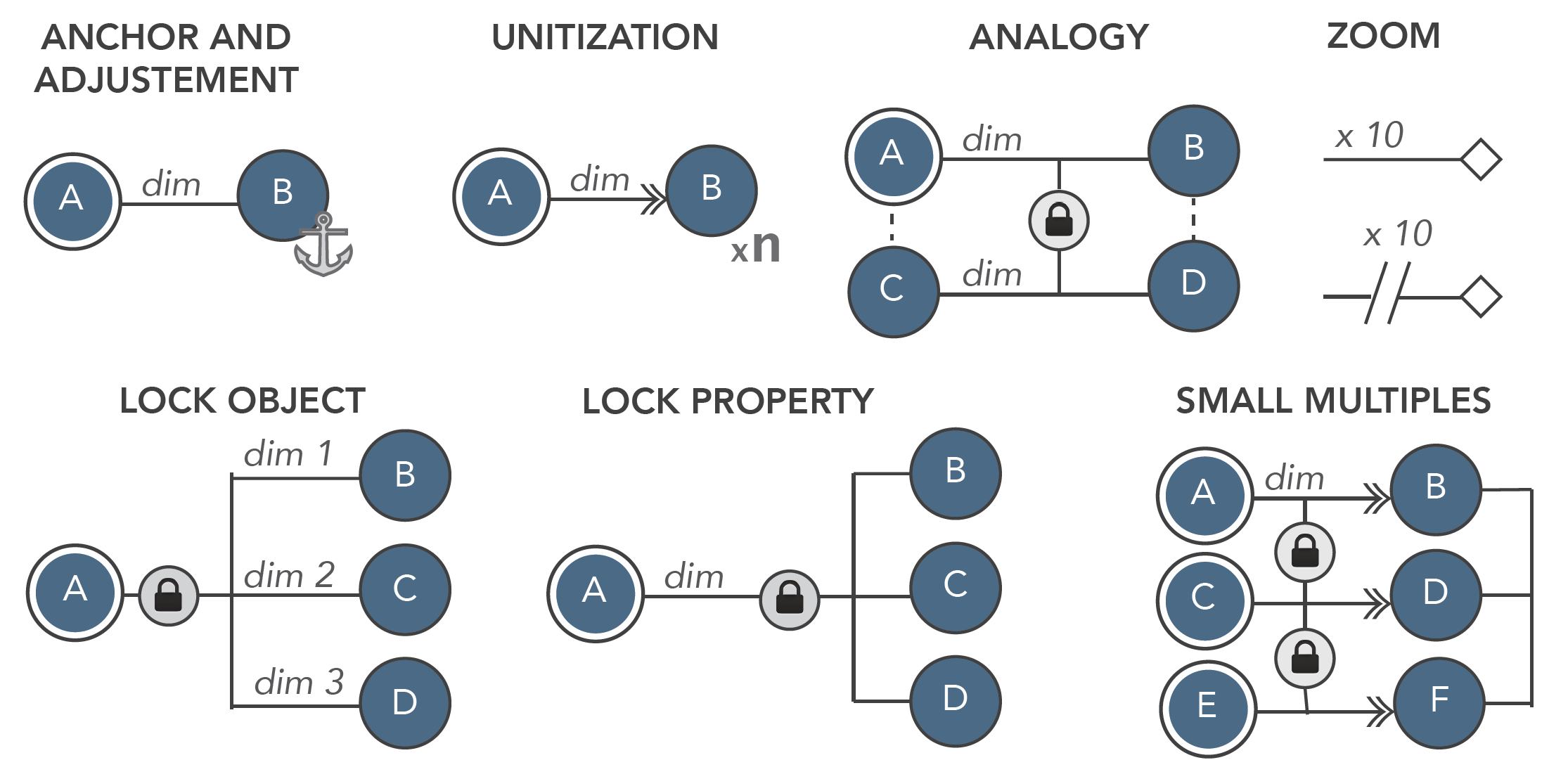
Measure Relations

Comparison

A comparison is a relation between objects that results in equality, inferiority, or superiority. There usually are types of comparisons: exact and approximate. Exact relations concern cases where magnitudes of objects can be accurately compared along a property (e.g., a $100 bill is 10 times superior than a $10 bill in terms of monetary value). Approximate is when the magnitudes are vaguely defined d (e.g, the height of an average person).

Containment

A containment is when objects are placed within a container, both objects become linked by a containment relation. Containers are common in concrete scales especially because they allow several objects into a single entity,which can facilitate comparison.

Unitization

A unitization is an improvised—yet subjective—systematization of units where observers can break down scales, using a preferred new unit, into more specific and relatable chunks.

Below is an illustration of super-massive black hole (complex measure) measured in suns (simple unit).

Analogy: Simultaneous Pairwise Comparison

An analogy conveys the size of relationships by comparing the size difference between a pair of objects, the target, and another pair of more familiar objects: the base.

Zoom

A zoom is the progressive adjustment and containment when the magnitude is too large to both see details on a relative scale while having an overview of the absolute scale. When the tools are dynamic, the zoom effect is executed through animation.

Lock

A lock strategy is the progressive adjustment and containment. The general idea builds on locking the possible relation of an object to a specific type as a constraint.

Small Multiples: Build a Collection

The small multiples are the small elementary objects juxtaposed together to aid in establishing a concrete scale through the use of a singular measure relation.

Visualizing the Scale of World Economies. Owen Cornec, Romain Vuillemot.

Romain Vuillemot